Predicting Options Call Pricing Using Machine Learning

Authors:

Muhammad Murtadha Ramadhan, Amrusha Buddhiraju, Chinmay Atul Sashittal, Evan Benham, Muskan Aggarwal, Vineetha Jinan

Background:

This project revolves around the valuation of European call options on the S&P 500 index. A European call option grants the holder the right, but not the obligation, to purchase an asset at a predetermined price, called the strike price, on a specific expiration date. These options are pivotal financial instruments used for hedging risk, speculative trading, and enhancing portfolio returns due to their leverage effect.

Traditionally, the Black-Scholes model has been a foundational tool for pricing European call options. Developed by Fischer Black and Myron Scholes in 1973, this model calculates the theoretical value of options using parameters such as the strike price, underlying asset price, volatility of the asset, time to expiration, and the risk-free rate of return. The model’s formulation is grounded in the assumption that the asset prices follow a geometric Brownian motion with constant drift and volatility. In 1997, the importance of the Black-Scholes model was recognized with the award of the Nobel Prize in Economics.

However, despite its widespread use and theoretical appeal, the Black-Scholes model has limitations, particularly in high-frequency trading environments where market conditions can change rapidly. It assumes volatility is constant and markets are static without accounting for more complex factors like varying interest rates, transaction costs, or divergences from the log-normal distribution of asset returns. These simplifications can lead to pricing errors, particularly for options that are far from expiration or deep in/out of the money.

Given these limitations, there is a growing interest in exploring alternative models and methodologies that incorporate more dynamic variables and better handle real-world market complexities. Machine learning approaches, for example, offer the potential to model option prices based on non-linear relationships and complex market dynamics that traditional models might not capture effectively. This project aims to explore such alternatives, comparing their performance against the Black-Scholes formula to potentially uncover more robust methods of option valuation.

Datasets:

The dataset focuses on European call option pricing data on the S&P 500, incorporating variables like current asset value (S), strike price (K), annual interest rate (r), and time to maturity (tau). For regression analysis, the dependent variable is the current option value (Value), and for classification analysis, it is the binary indicator (BS), denoting whether the option's value prediction is over or under the actual value. The dataset includes a training set with detailed records for each option, and a testing set without labels for Value and BS, intended to validate the performance of machine learning models developed from the training data.

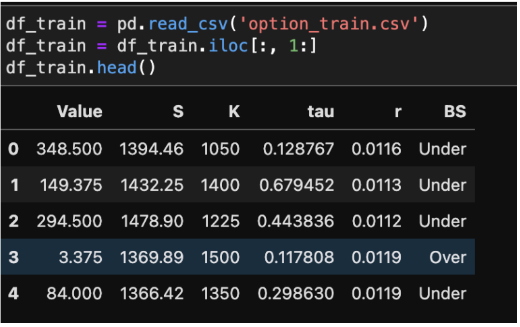
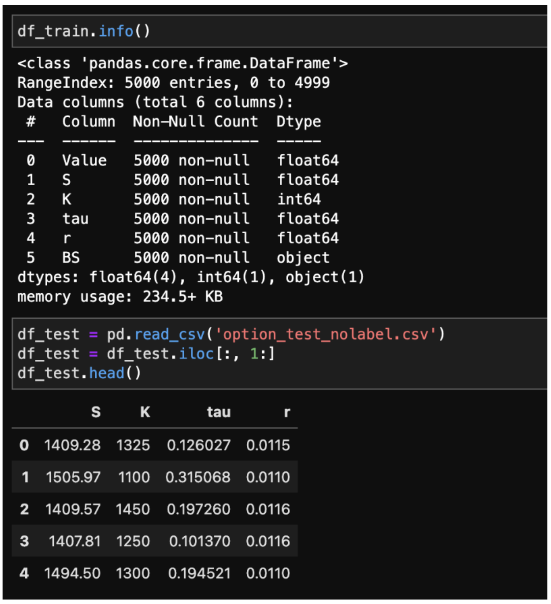
Data Preprocessing

During the data processing phase, multiple steps were undertaken to prepare the data for analysis. These included exploratory data analysis, checking for missing values to ensure data completeness and standardizing data to maintain consistency across the dataset.

• Missing value check: Upon examination of both the train and test datasets, it was found that there was no missing data in any of the columns. As a result, there was no need for imputation to fill in missing values.
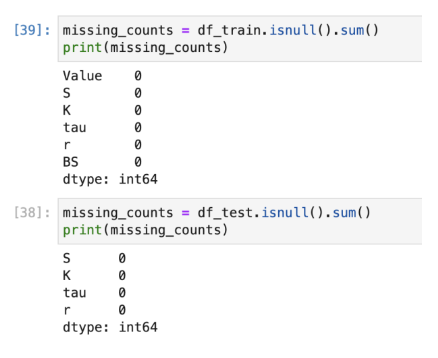
• Data Standardization: Before proceeding with further analysis, data standardization was also carried out. This step ensured that the dataset had a uniform scale, enhancing the reliability of any analytical methods applied later. Standardizing the data helped in comparing features that had different units or scales effectively.

Regression Analysis

After preprocessing, the dataset was ready for the data modeling process. To have a robust modeling process, 10-fold cross-validation (10-fold CV) was also implemented. Then, initial data modeling was performed for several algorithms which were Linear Regression, Random Forest, KNN Regression, and Support Vector Regression with default hyperparameters used in each algorithm. To test model performance initially, we used the validation set approach by splitting the available training data into test and train datasets (20% test and 80% train).

• Linear Regression: Linear regression is a simple yet powerful algorithm that assumes a linear relationship between the input features and the target variable.
  • Performance: The initial modeling using linear regression yielded a mean R-squared score of 92.44% from cross-validation. While linear regression is straightforward and easy to interpret, its performance may be limited due to potential multicollinearity caused by the correlated variables.
• Random Forest Regression: Random forest regression is an ensemble learning method that builds multiple decision trees during training and outputs the mean prediction of the individual trees. Its ability to handle non-linear relationships and feature interactions made it an ideal choice.
  • Performance: Random forest regression demonstrated superior performance compared to other algorithms, achieving an impressive mean R-squared score of 99.66%.
• KNN Regression: K-nearest neighbors (KNN) regression is a non-parametric algorithm that predicts the target variable by averaging the values of its k-nearest neighbors in the feature space.
  • Performance: KNN regression performed reasonably well, yielding a mean R-squared score of 94.82% from cross-validation.
• Support Vector Regression (SVR): Support vector regression is a supervised learning algorithm that finds the optimal hyperplane in a high-dimensional space to minimize the error between the predicted and actual values. SVR can handle non-linear relationships through the use of kernel functions
  • Performance: SVR exhibited the lowest performance among the algorithms considered, with a mean R-squared score of 59.15% from cross-validation.

From the initial modeling result, it can be seen that Random Forest Regression outperformed all other algorithms with an R-squared score of 99.66%. Then, hyperparameter tuning for each algorithm was performed to fine-tune the model as well as to find the best hyperparameter for prediction. The method used for hyperparameter tuning in this case was GridSearch Cross Validation.

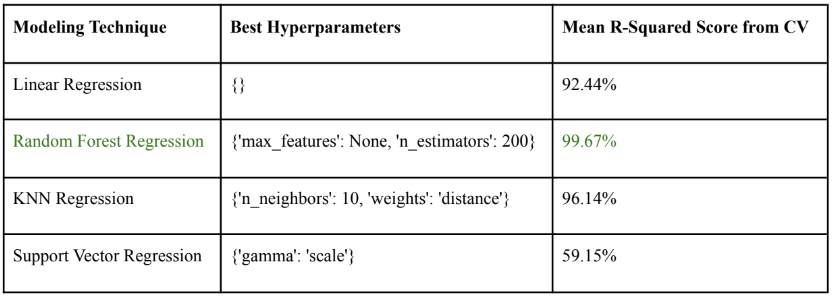
From the hyperparameter tuning process, it can be observed that Random Forest Regression still outperformed the other algorithms in terms of R-squared score performance with the optimal hyperparameters making it our final choice for Value prediction.

Classification Analysis

For predicting the binary status (BS) of over or underestimation in European call option pricing, we evaluated Logistic Regression, Random Forest Classifier, Support Vector Machine (SVM), and K-Nearest Neighbors (KNN) Classifier methods. We tested the performance of these approaches, by comparing their classification errors. To do this, we used the validation set approach by splitting the available training data into test and train datasets (20% test and 80% train).

• Logistic Regression: Logistic regression is a linear model used for binary classification tasks, estimating the probability of a binary outcome based on one or more predictor variables. It was considered due to its straightforward application in binary classification tasks and its ability to provide probabilities, which are useful for threshold tuning.
  • Performance: Logistic regression achieved a classification error rate of 12.26%.
• Random Forest Classifier: Random forest classifier is an ensemble learning method that constructs multiple decision trees during training and outputs the mode of the classes (for classification tasks) of the individual trees. Its ability to handle complex relationships and reduce overfitting through ensemble learning made it highly suitable for this task.
  • Performance: Random forest classifier demonstrated the best performance, with a classification error rate of 6.36%.
• Support Vector Machine (SVM): SVM is a supervised learning algorithm that finds the optimal hyperplane to separate data points into different classes in a high-dimensional space. It was chosen for its robustness in high-dimensional spaces.
  • Performance: SVM exhibited a classification error rate of 15.8%.
• K-Nearest Neighbors (KNN) Classifier: KNN classifier is a simple and interpretable non-parametric algorithm that assigns a class label to an instance based on the majority class of its k nearest neighbors in the feature space.
  • Performance: KNN classifier achieved a classification error rate of 14.76%. This selection process was crucial in ensuring we chose the most suitable model for our classification needs, with the Random Forest ultimately standing out due to its low error rate and robust performance across various metrics.

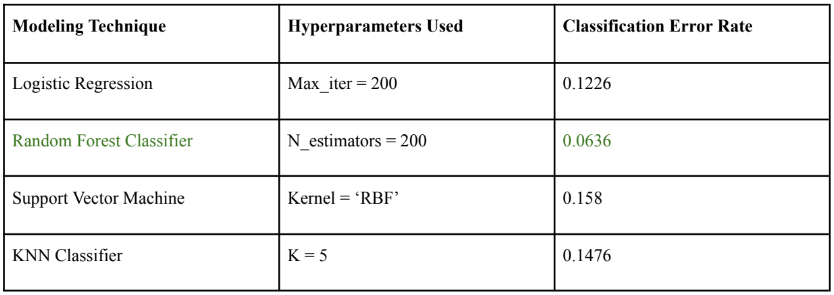
We see that the Random Forest Error classifier with 200 estimators gave us the lowest classification error of 6.36% meaning that only 6.36% of options would be misclassified. When it comes to predicting European call option pricing, accuracy is the highest priority, leading us to random forest classifier as our final choice for predicting BS over/under prediction. Beyond classification error, Random forest has the following advantages over other models:

• Robustness to Overfitting and Reduced Variance: By aggregating the predictions of multiple decision trees, Random Forests are less prone to overfitting and have lower variance.
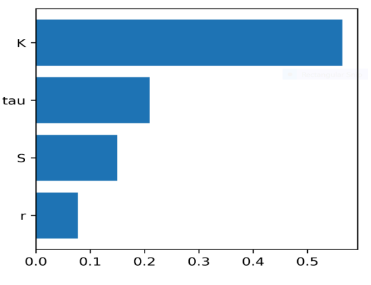
• Feature Importance: By evaluating feature importance based on how much each feature decreases impurity across all trees, Random Forests provide insights into which features are critical for classification.

The classification prediction can further be improved by using ensemble methods that combine multiple Random Forest models or other types of models to boost performance further.

Business Impact

Leveraging machine learning models for option pricing compared to the traditional Black-Scholes formula has the following business implications and considerations for real-world application :

• Including All Predictor Variables: Initially, including all four predictor variables (current asset value, strike price, interest rate, and time to maturity) can be advantageous. This allows the model to identify which factors have the most significant influence on option pricing. Subsequently, feature selection techniques can be employed to pinpoint the most impactful variables, potentially enhancing model efficiency.
• Machine learning vs. Black-Scholes: ML models can outperform the Black-Scholes formula in predicting option values due to their ability to capture complex relationships between multiple variables and the option price that may be neglected otherwise. The Black-Scholes formula relies on assumptions that may not always reflect real-world market conditions. While machine learning models can achieve higher accuracy by learning complex patterns from historical data, this complexity can lead to models that are difficult to interpret and computationally expensive to run. Additionally, models trained on historical data may not generalize well to unseen market conditions.
• Model applicability to new stocks: Directly applying the trained model to new stocks is not ideal. The model is trained on historical data, and market dynamics can evolve considerably. Before applying the model to a specific stock like Tesla, it's advisable to first assess its performance on unseen data from the same asset class (S&P 500). Additionally, incorporating domain knowledge about the stock market and Tesla specifically could further refine the model's accuracy.
• Prediction Accuracy vs. Interpretability: In the context of option pricing, prediction accuracy holds greater significance than interpretability. Options are financial instruments used for managing risk and speculation. Even minor pricing errors can result in substantial financial losses. While understanding how the model arrives at a prediction can be valuable (interpretability), it's less critical than the model's ability to deliver a correct option value.

Conclusion

The analysis revealed that machine learning models are a viable alternative to the traditional Black-Scholes formula, particularly when dealing with complex market dynamics. However, there's room for further exploration & optimization:

• Segmentation and Specialized Models: Stock options exhibit diverse behaviors based on underlying assets, maturities, and market conditions. Future work could involve segmenting options based on similar characteristics and building specialized predictor models for each segment. This approach could potentially improve overall accuracy by introducing a balance of specificity and generalizability within the segment.
• Ensemble Models: Combining the strengths of traditional models, like Black-Scholes, and modern machine learning models could lead to more accurate predictions.
• Incorporating Market Sentiment: Option pricing is influenced not only by fundamental factors but also by market sentiment and broader economic trends. Integrating advanced language models capable of analyzing news articles, social media data, and other textual sources could enable more holistic prediction models that account for these intangible factors.

By pursuing these avenues for improvement, we can further refine option pricing models, leading to more informed financial decisions and potentially reducing risk in the options market.